❒ Description
DB 인덱스는 B-tree 자료구조를 사용한다. (참고로 MySQL은 B+tree)
B-tree와 조회,삽입,삭제의 시간복잡도가 동일한 다른 self-balancing BST인 AVL, Red-Black tree도 있는데
왜 B-tree를 쓰는지 알고는 있지만 개념을 정리해보자.
❒ 메모리 계층
우선 DB가 어디서 데이터를 퍼올리는지 이해해야 한다.
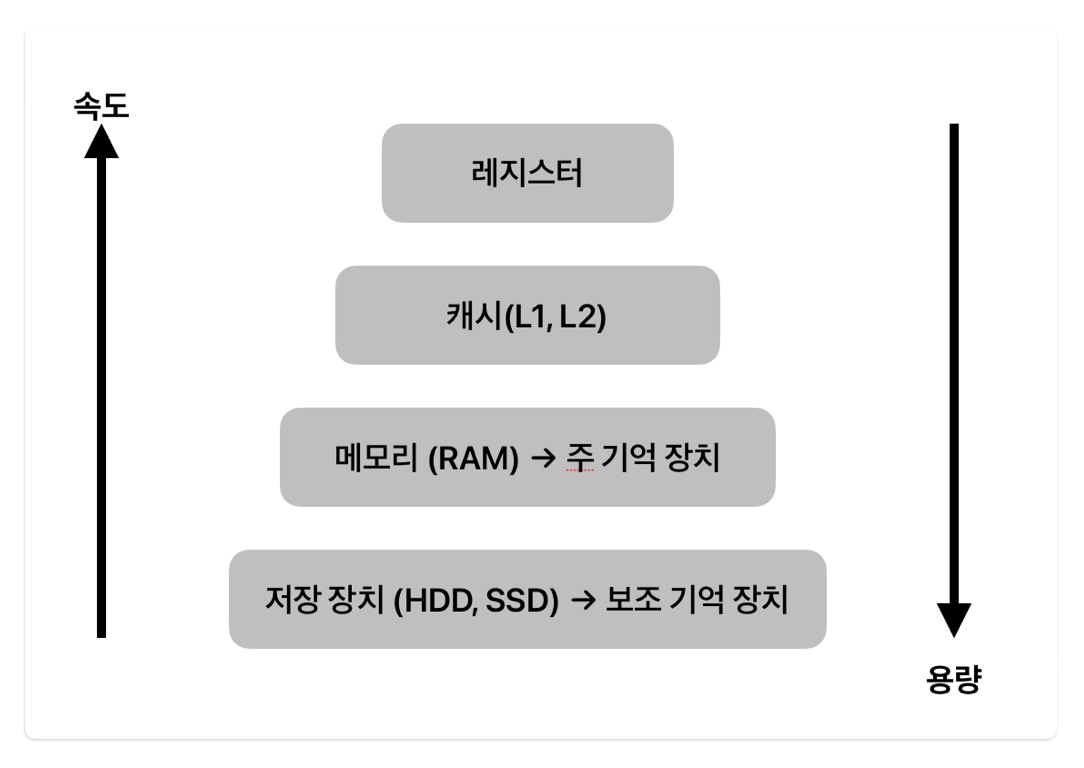
위 이미지는 메모리 계층을 나타낸 것이다. 위로 올라갈 수록 속도는 빨라지지만 용량은 작아진다. 우리가 DB에
저장하는 데이터는 가장 하위에 위치한 보조 기억 장치에 저장된다. 보조 기억 장치와 주 기억 장치 사이의 데이터
전송 단위를 Block이라고 하는데, 딱 원하는 데이터만 읽어 오는 것은 아니고 한 block 단위로 데이터를 읽어온다.
결국 DB에 있는 데이터는 보조 기억 장치에 저장이 된다. 따라서 데이터를 조회할 때도 보조 기억 장치에서 조회를
해서 주 기억 장치에 데이터를 전송하게 된다. 매번 보조 기억 장치에 접근하면 당연히 성능이 저하될 수 밖에 없다.
데이터베이스 조회 성능을 향상 시키기 위해서는 보조 기억 장치에 접근 하는 횟수를 최소한으로 줄여줘야 한다.
또한 데이터를 block 단위로 전송한다고 했다. 이때, 한 block에 연관되 데이터가 모여있다면 더 효율적으로 읽고
쓸 수 있을 것이다.
❒ B - tree
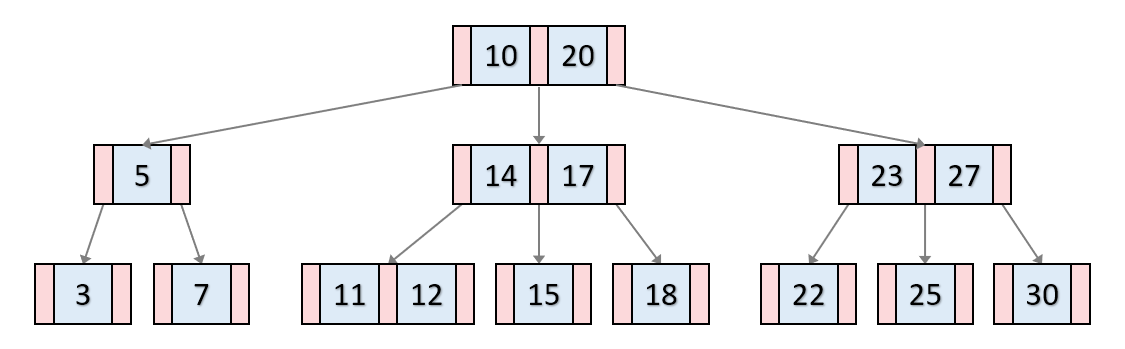
1. 정의
B-Tree란 Balanced Tree로 균형을 유지하는 tree를 의미하며 BST를 일반화한 tree다.
하지만 이진트리와는 달리 하나의 노드가 여러 데이터를 가질 수 있다.
- 자녀 노드의 최대 개수를 늘리기 위해서 부모 노드에 key를 하나 이상 저장한다.
- 부모 노드의 key들을 오름차순으로 정렬한다.
- 정렬된 순서에 따라 자녀 노드들의 key값의 범위가 정해진다.
- 노드의 데이터 수 가 N이면 자식의 수는 항상 N + 1이 되어야 한다.
- 추가는 항상 leaf 노드에 한다.
- 노드가 넘치면 가운데 키를 기준으로 좌우 키들은 분할하고, 가운데 키는 승진한다.
2. 주요 파라미터
| 파라미터 | 설명 | 특이점 |
| M | 각 노드의 최대 자녀 노드 수 | |
| M - 1 | 각 노드의 최대 key 수 | |
| ⎡M / 2⎤ | 각 노드의 최소 자녀 노드 수 | 루트 노드, 리프 노드에서는 적용되지 않는 조건 |
| ⎡M / 2⎤- 1 | 각 노드의 최소 key 수 | 루트 노드에서는 적용되지 않는 조건 |
❒ 그럼 왜 B-tree 계열을 DB 인덱스로 쓰는 걸까?
위에 정리한 메모리 계층을 보면 쉽게 이해할 수 있다. B-tree는 하나의 노드에 여러 개의 key를 저장할 수 있다.
즉, DB 데이터가 저장되어 있는 보조기억 장치에 접근하는 횟수가 다른 tree 계열 자료구조 보다 적다는 것을
의미한다. 또한 노드에 연속적인 값이 정렬되어 저장되기 때문에 Block 단위의 대한 저장 공간 활용도가 더 좋다는
장점이 있다.
물론 hash index도 사용할 수 있겠지만, hash index의 경우에는 `equality(=)` 조회만 가능하고,
범위 기반의 검색이나 정렬에는 사용할 수 없다는 단점이 있기 때문에 사용하지 않는다.
❒ B+tree
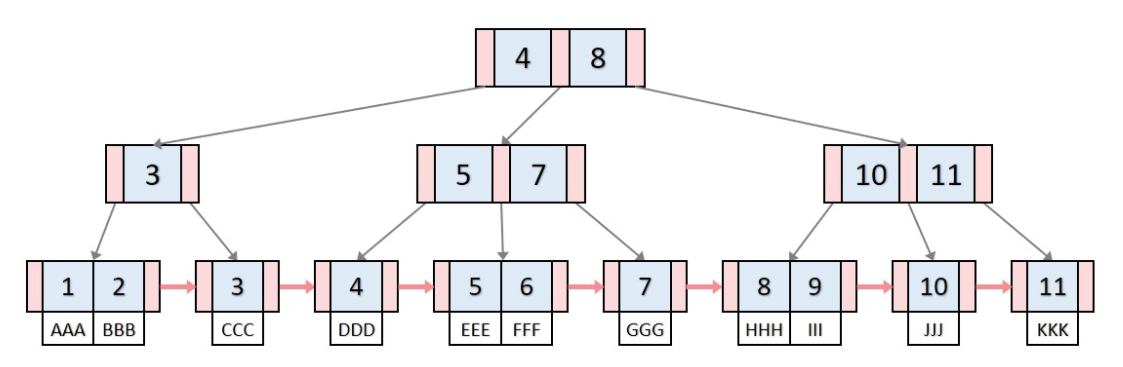
"B+Tree"는 B-Tree의 확장개념으로, 리프 노드를 제외하고 데이터를 담아두지 않기 때문에 메모리를 더
확보함으로써 더 많은 key들을 수용할 수 있다. 결과적으로 하나의 노드에 더 많은 key들을 담을 수 있기
때문에 트리의 높이는 더 낮아지며, cache hit 확률은 더 높일 수 있다.
또한 Full Scan 시, B+tree는 리프 노드에 데이터가 모두 있기 때문에 한 번의 선형탐색만 하면 되기 때문에
B-tree에 비해 빠르다. 반면 B-tree의 경우에는 모든 노드를 확인해야 한다.
'CS > Database' 카테고리의 다른 글
| Lock을 활용한 concurrency control (0) | 2024.10.02 |
|---|---|
| Isolation 레벨과 이상 현상들 (0) | 2024.09.26 |
| DB Transaction & Concurreny Control (2) (0) | 2024.09.20 |
| DB Transaction & Concurreny Control (1) (0) | 2024.09.12 |
| FD & Normalization (0) | 2024.09.01 |