❒ Description
| 날짜 | 2024.10.01 (화) |
| 레벨 | Medium |
| 제목 | Search in Rotated Sorted Array |
| 링크 | https://leetcode.com/problems/search-in-rotated-sorted-array/description |
| 알고리즘 | Binary Search |
| 시간 복잡도 | O(logN) |
❒ 문제 및 로직 분석
이 문제는 O(logN)의 시간 복잡도로 풀이해야 하는 문제로, pivot을 기준으로 회전된 정렬 배열에서
특정 값을 찾아야 한다.
int[] nums = {4, 5, 6, 7, 0, 1, 2, 3};
1. Pivot 찾는 방식
먼저 pivot을 찾아야 한다. 시간복잡도 제약이 있기 때문에 pivot을 찾는 과정도 O(logN)로 해결해야 한다.
Pivot을 찾으려면 `nums[p - 1] > nums[p]` 이 조건이 성립해야 한다.
이렇게 pivot을 찾은 후, pivot을 기준으로 좌,우 배열을 binary search 하면서 값을 도출하면된다.
2. Pivot 찾지 않는 방식
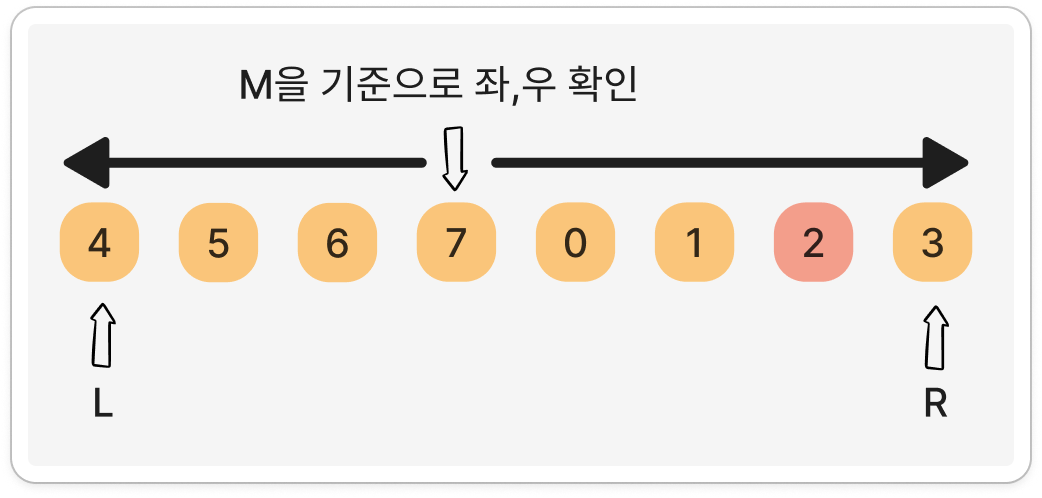
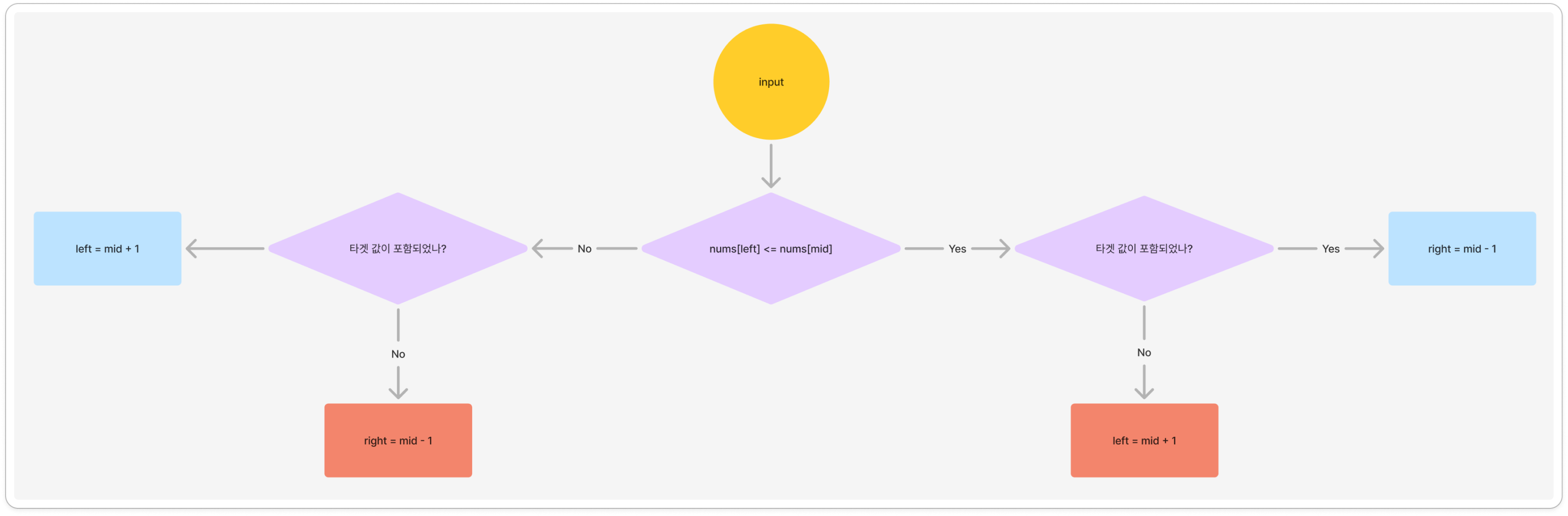
❒ Solution
1. Pivot 찾는 방식
public int search(int[] nums, int target) {
int pivot = findPivot(nums);
int leftResult = binarySearch(nums, 0, pivot -1, target);
if (leftResult > -1) {
return leftResult;
}
return binarySearch(nums, pivot, nums.length - 1, target);
}
private int findPivot(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (mid > 0 && nums[mid - 1] > nums[mid]) {
return mid;
} else if (nums[0] <= nums[mid]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return 0;
}
private int binarySearch(int[] nums, int left, int right, int target) {
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] < target) {
left = mid + 1;
} else if (nums[mid] > target) {
right = mid - 1;
} else {
return mid;
}
}
return -1;
}
2. Pivot 찾지 않는 방식
public int search(int[] nums, int target) {
int left = 0;
int right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (nums[mid] == target) return mid;
if (nums[left] <= nums[mid]) {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
'Algorithm > 문제풀이' 카테고리의 다른 글
| [Programmers] 입국심사 (0) | 2024.10.21 |
|---|---|
| [LeetCode#74] Search a 2D Matrix (0) | 2024.10.02 |
| [LeetCode#75] Sort Colors (0) | 2024.10.01 |
| [LeetCode#242] Valid Anagram (0) | 2024.09.29 |
| [LeetCode#179] Largest Number (0) | 2024.09.29 |