❐ Description
[LeetCode#162] Find Peak Element 문제를 풀면서 단순하게 생각했던 부분을 바로 잡자.
❐ Find Peak Element
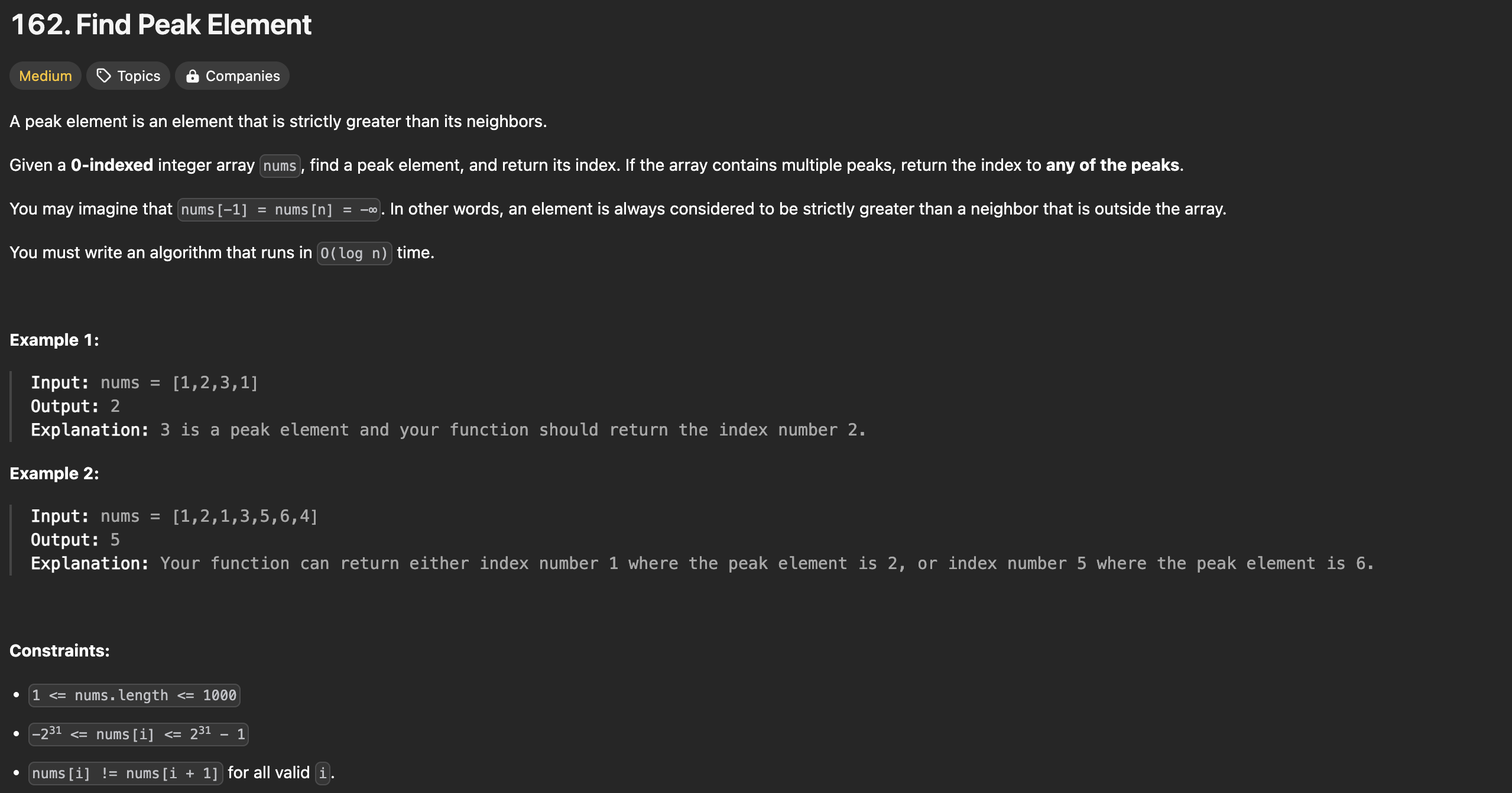
이진 탐색이란 오름차순으로 정렬된 리스트에서 단조성을 이용해 특정값을 찾는 알고리즘이다. (wiki 링크)
단조성이란? 값이 한 방향으로 증가하거나 감소하는 특성
그래서 이 문제를 처음에 접근할 때 이진 트리를 어떻게 사용하라는 거지? 라는 생각을 헀다.
왜냐면 주어진 배열은 오름차순이 아니기 때문이다. 하지만 해당 문제의 요구사항 중 하나는
`O(logN)`의 시간 복잡도로 풀이를 하는 것이다.
❐ 정렬되어 있지 않아도 Binary Search를 적용할 수 있다.
위에서 단조성에 대해서 이야기 했다. 그럼 다음 배열은 단조성을 띄고 있는가?
int[] array = {1, 2, 1, 3, 5, 6, 4};그렇지 않다. 한 방향으로 증가하지도, 감소하지도 않는다.
여기서 쫌 더 꼼꼼히 생각해보자. 배열을 좀 더 확대해서 보면 어떨까?
{1,2} {2,1} {1,3} {3,5} {5,6} {6,4}각 집합은 모두 단조성을 갖는다.
결과적으로 이 문제를 해결하기 위해서는 주어진 배열을 쪼개서 볼 줄 알아야 한다.
즉, 부분적인 단조성을 활용해서 이 문제를 해결해야 하는 것이다.
이러한 특성 덕분에 이진 탐색은 정렬된 배열뿐 아니라 다양한 변형 문제에서도 많이 활용된다고 한다.
❐ 부분 단조성을 사용해서 풀어보기

- 주어진 배열에서 `mid`를 시작으로 하고 `mid+1`을 끝으로하는 부분 배열을 확인한다.
- `mid`가 `mid + 1`보다 크거나 같은 경우
- 감소 구간 (단조 감소)
- 피크 요소는 왼쪽 또는 현재 mid에 있을 수 있다.
- `mid`가 `mid + 1`보다 크거나 같은 경우
- 증가 구간 (단조 증가)
- 피크 요소는 오른쪽에 있을 수 있다.
public calss Solution {
public int findPeakElement(int[] nums) {
int left = 0;
int right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] >= nums[mid + 1]) {
right = mid;
}
left = mid + 1;
}
return left;
}
}
'Algorithm > 내용 정리' 카테고리의 다른 글
| Counting Sort (0) | 2025.01.21 |
|---|---|
| Memoization (메모이제이션) (0) | 2025.01.09 |
| Manacher 알고리즘 (0) | 2024.12.15 |
| Back Tracking (0) | 2024.11.20 |
| Binary Search (0) | 2024.10.01 |